Tutorial II: "Schöne Graphen "

5.2 Tutorial II: "Schöne Graphen "
	Schönheit muß von innen kommen und gerade Graphen zeigen dies. Sie fußen auf dem menschlichen Bedürfnis nach Zweisamkeit. Oder hat jemand schon zwei Leuten gleichzeitig die Hand gegeben? Stellen wir uns eine Party mit 12 Gästen vor, die an einen runden Tisch sitzen (Kopieren Sie diese Zeilen einfach in die TGL-Main-Console).

proc round-table {s x y r} {
    upvar pi pi
    set q [$s get graph]
    set n [$s count]
    for {set i 1} {$i <= $n} {incr i} {
        $q.coords set attribute   \
            "as $s index $i"        \
        [list [expr $x + $r*cos(2.0*$i/$n*$pi)] \
              [expr $y + $r*sin(2.0*$i/$n*$pi)]]
    }
}

Graph0.all erase
Graph0 new node 12
round-table Graph0.nodes 300 300 230

Auf dieser Party wollen sich jetzt alle die Hand reichen.

proc complete { s } {
set q [$s get graph]
    set n [$s count]
    for {set i 1} {$i < $n} {incr i} {
      $q new undirected edge \
             "as $s index $i" \
             "as $s index [expr $i+1] $n"
    }
}
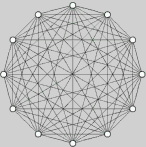
complete Graph0.nodes

Dies ist ein vollständiger Graph.

Wie häufig werden insgesamt Hände gereicht. Bevor wir lange überlegen, daß jeder elf anderen die Hand reicht und wir die dadurch jedes Händeschütteln doppelt gezählt haben, lassen wir zählen:

Graph0.edges count

Dieser Befehl setzt die Koordinaten aller Knoten auf {200 200}.

Natürlich gibt es auch größere Feiern:

Graph0.all erase
Graph0 new node 30
round-table Graph0.nodes 300 300 230
complete Graph0.nodes

Beim Shake-Hands im Falle von Fußballmannschaften, ändert sich das Prinzip:

proc line {s x1 y1 x2 y2} {
    set q [$s get graph]
    set n [$s count]
    for {set i 0} {$i < $n} {incr i} {
        $q.coords set attribute   \
            "as $s index [expr $i+1]"        \
       [list [expr $x1 + $i*($x2-$x1)/($n-1)]\
             [expr $y1 + $i*($y2-$y1)/($n-1)]]
    }
}

Graph0.all erase
Graph0 new as name heim
Graph0 new node 11 in heim
line Graph0.heim 100 100 500 100

Die Heimmannschaft:

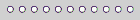Die Gastmannschaft in Rot:

Graph0 new as name gast
Graph0.node_fillcolor set default red
Graph0 new node 11 in gast
Graph0.node_fillcolor set default white
line Graph0.gast 100 500 500 500

Shake-Hands

Graph0 new undirected edge {as heim} {as gast}

Soviel zum Sport und zurück zur Natur:

Graph0 new as name height
Graph0 new as name root
proc tree {r d x0 y0 a s} {
upvar pi pi; upvar b1 b1;
upvar b2 b2; upvar f1 f1;
upvar f2 f2
set x [expr $x0+$s*cos($pi*$a/180)]
set y [expr $y0+$s*sin($pi*$a/180)]
Graph0.coords set default [list $x $y]
Graph0 new node in $r with height $d
if {$d > 0} {
      set son [Graph0 new as]
      tree $son [expr $d-1] $x $y [expr $a+$b1] [expr $s*$f1]
      Graph0 new directed edge "as $r" "as $son" with height $d
      $son = {as none}
      tree $son [expr $d-1] $x $y [expr $a+$b2] [expr $s*$f2]
      Graph0 new directed edge "as $r" "as $son" with height $d
      $son delete
}
}

Sie werden sich jetzt sicher fragen, was dieses Programm wohl macht. Nehmen Sie sich das als warnendes Beispiel und kommentieren Sie Ihre Programm(schnips)e(l) sorgfältig für die Nachwelt (so wie ich...).

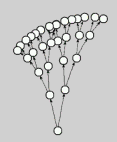
Die Auflösung naht... Das ist ein Baum:

set b1 10; set b2 -13; set f1 0.8; set f2 0.7
Graph0.nodes erase
tree Graph0.root 4 300 500 -90 130

Nun ja. Ziemlich knotig, der Baum. Wir werden ihn etwas liften:

Graph0.node_fillcolor set attribute \
"as height matches 1 4" black
Graph0.node_fillcolor set attribute \
"as height matches 1" green

for {set i 1} {$i <= [Graph0.edges count]} \
       {incr i} {
   set w [Graph0.height min \
         "as Graph0.edges index $i"]
   Graph0.edge_width set attribute
     "as Graph0.edges index $i" [expr 3*$w+4]
}

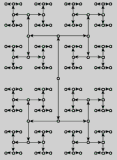
Für die (Graphen-) Theorie ist der folgende Baum genau dasselbe wie eben nur größer.

set  b1 90; set b2 -90
set f1 [expr pow(0.5,0.5)]; set  f2 $f1
Graph0.nodes erase
Graph0.node_size set default 3
tree Graph0.root 6 10 200 0 150

Es entsteht wiederum eine Schleife und eine Kante vom dritten Typ, der zur Verfügung steht: die ungerichtete Kante.

5.2 Tutorial II: "Schöne Graphen "